How to draw a square in perspective

Question from Daniel Michalovics, Drawing Academy student

Hi,

My name is Daniel. I live in Germany and I am glad that I have finally arrived at the Drawing Academy. I am currently working on Drawing in Perspective.

At this point, I must mention that when enrolling in the Drawing Academy, I did not know that there was a proposed list of assignments. However, I find this extremely helpful. The assignments seem to be in an order that is very easy to follow. I really appreciate this curriculum because in the past, I tried to make my own assignment list which was nowhere near as logical and target-oriented as the one found here. This one really encourages me to work hard on my drawing skills.

Here is my actual question. I tried to draw an imaginary set of pyramids with squares at their bottoms in a one-point perspective. How do I know how long I need to draw the edge of a square that is facing towards the vanishing point?

It must have some specific length so that the bottom plane is seen as a square with equal side lengths. From the rules of perspective, I know that this line must be shorter than the horizontal line at the front. However, when drawing from imagination, I can only guess its real length. Is there some kind of trick I can apply here?

I have seen a few internet videos that teach how to draw a perfect cube in a two-point perspective. However, the methods they show are rather complex. I prefer not to use them every time I try to draw a simple square. I also do not like the fact that these methods only cover a two-point perspective. If there is no simple method, how can I learn to estimate the length correctly?

Dear Daniel,

Many thanks for your kind words about the Drawing Academy course. I am glad you found it helpful and the assignment list useful.

For a very long time, fine artists have found the topic of drawing in perspective to be fascinating. The Old Masters meticulously studied the one-point and two-point perspectives.

To answer your question, yes, there are several methods that can be used to determine the depth of a square in a one-point perspective. Below, I will describe the simplest one.

However, before we go into details, I want to say that you don’t have to do such a calculation every time you draw an object in perspective.

As a fine artist, you have a license to draw imaginary objects as you see them in your head. You do not need to craft geometrically perfect outlines with a ruler and compass.

Your proficient drawing skills depend on your ability to draw freehand. They do not depend on the use of tricks and measurement instruments. It is important, to your creative development, to practice sketching and drawing from your imagination.

With this in mind, we can now examine a ways of “calculating” the depth of a square in a one-point perspective.

The One-Point Perspective Method

On the image below, an artist looks at the red square lying on the ground.

We see this square from the side, so it appears to us as a thick red line. The image is sight-projected onto the canvas or drawing board, which is located in front of an artist.

In this case, the size of the square drawing will depend on three measurements – the distance between the eye line (which always coincides with the horizon level), the distance between the artist’s eyes and the drawing board, and the distance between the drawing and the object itself.

The scale of the object will depend on the location of the drawing board while relative proportions of the object’s dimensions will remain the same. This calculation is applicable when you draw using the “sight-size” method.

When drawing from your imagination, you can still use such a method. You can mentally reconstruct the studio environment as if you are drawing from life. All you need to do is make a quick sketch:

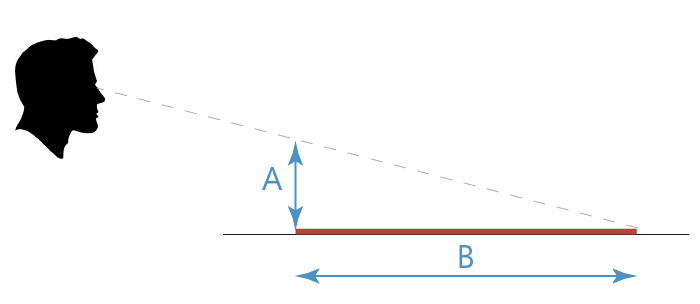
Of course, the artist’s head silhouette is optional : )

The main point of this sketch is to determine the angle from which the square is viewed (the tilt of the diagonal line). In other words, this angle is how close or far from the horizon line the object is. This angle will define the dimension marked by “A.” The closer the square is to the horizon level, the sharper the angle and the smaller the dimension “A” will be.

Now, all you need to do is to check the proportion of “A” to “B” (or how many times “A” fits into “B”). With all sides of the square equal, we can substitute its width for height in our example.

Finally, make sure your drawing of a square in a one-point perspective has the same ratio.

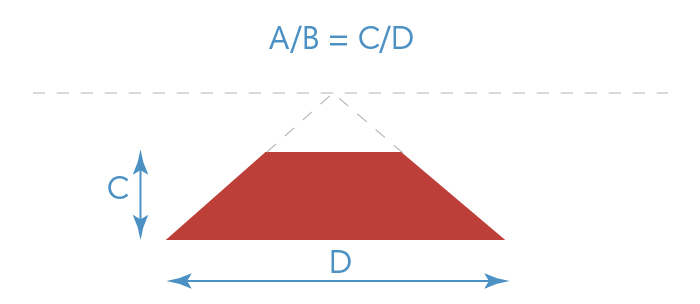
On the image above, you can see that the red square in perspective has the same ratio of the square’s depth to width (marked as “C” to “D”) as the ratio A/B.

I hope this helps and that the method is simple enough to achieve certain precision in your drawing.

In any case, I would suggest you develop a the skill of measuring proportions by eye and feel what is right and looks natural and realistic when drawing.

Let me know if you have any other questions. I will be happy to help.

Kind regards,
Vladimir

To learn how to draw skillfully,